MATRICES
The concept of matrices was developed by a Mathematician Arthur Cayley . Matrices are useful in expressing numerical information in compact form. They are effectively used in expressing different operators .
Definition :
A rectangular arrangememnt of mn numbers in m rows and n columns, emclosed in [ ] or ( ) is called a matrix of order m by n .
A matrix by itself does not have a value or any special meaning . Order of the matrix is denoted by m m🗙n , read as m by n . Each member of the matrix is called an element of the matrix . Matrices are generaly denoted by A, B, C, ... and their elements are denoted by aij ,bij , cij , ...etc.
Matrix is generaly written as :
Important Formulas for Matrices
If A and B are square matrices of order n, and In is a corresponding unit matrix , then
(a) A(adj.A) = | A | In = (adj A) A
(b) | adj A | = | A |n-1 (Thus A (adj A) is always a scalar matrix)
(c) adj (adj.A) = | A |n-2 A
(d) adj (AB) = (adj B) (adj A)
(e) adj (Am) = (adj A)m,
(f) adj 0 = 0
(g) A is symmetric ⇒adj A is also symmetric
(h) A is diagonal ⇒adj A is also diagonal
(i) A is triangular ⇒adj A is also triangular
(j) A is singular ⇒| adj A | = 0
(k) | adj(adj.A)| = |A|(n-1)(n-1)
(l) adj(k A) = K n-1 (adj A) , k ∈ R
(m) adj(In ) = In.
Types Of Matrix :
1. Row Matrix:
A matrix having only one row is called as a row matrix . It is of order 1x n , where n ≥1 . ex., i) [2 5] ii) [2 3 6] .
2. Column Matrix :
A matrix having only one column is called as a column matrix . It is of order m x 1 , where m ≥1 .
3. Zero or Null Matrix :
A matrix in which every element of matrix is zero is callled as a zero or null matrix . It is denoted by 0.
4. Square Matrix :
A matrix with equal number of rows and column is called as a square matrix .
5. Diagonal Matrix :
A square matrix in which every non-diagonal elememt is zero ,is called as a diagonal matrix .
Note : If a11 ,b22 , c33 are diagonal element of a diagonal matrix A of order 3 , then we write the matrix A as A = Diag.
6. Scalar Matrix :
A diagonal matrix in which all the diagonal elements are same , is called as a scalar matrix .
7. Unit or Identity Matrix :
A scalar matrix in which all the diagonal elements are 1 (unity) , is callled as identity matrix of order n is denoted by In.
Note : i) Every identity matrix is scalar matrix but every scalar matrix is need not be identity matrix . ii) Every scalar matrix is diagonal matrix but every diagonal matrix need not be a scalar matrix.
8. Uppper Trigular Matrix :
A square matrix in which every element below the diagonal is zero , is callled as upper trigular matrix .
9. Lower Trigular Matrix :
A square matrix in ewhich every element above the diagonal is zero , is called as lower triular matrix .
10. Trigular Matrix :
A square matrix is called as trigular matrix if it is an uppper trigular or a lower trigular matrix.
Note: The diaggonal , unit and null matrices are also trigular matrix.
11. Symmetric Matrix:
A square matrix A = [ aij]nn in which aij = aji for all i and j , is called a symmentric matrix .
12. Skew - Symmetric Matrix :
A square matrix A= [ aij]nn in which aij = -ajifor all i and j , is called a skew - symmetric matrix. In skew -symmetric matrix each diagonal element is zero.
13. Determinant of a Matrix :
Determinant of a matrix is defined only for a square matrix . If A is a square matrix , then the same arrangement of as also gives us a determinant , by replacing square brackets by vertical bars. It s denoted by |A| or det(A) . If A =[ aij]nn then is pf order n.
14. SIngular Matrix :
A square matrix A is said to be singular matrix if |A| = det(A) = 0 , otherwise it is said to be non-singualr matrix.
15. Transpose of a Matrix :
The matrix obtained by interchanging rows and columns of matrix A is called as Trnaspose of matrix A . It is denoted by A' or AT.
eg.,

Properties of Transpose of Matrix
(i) (AT)T= A (ii) (A + B)T = AT+ BT (iii) (AB)T = BTAT (iv) (kA)T = k(A)T
(v) (A1A2A3 ……An-1An)T =
(vi) IT = I (vii) tr(A) = tr(AT)
16. Hermitian and skew – Hermitian matrix:
A = Aθ (Hermitian matrix)(Aθ represents conjugate transpose)
Aθ = -A (skew-Hermitian matrix).
17. Orthogonal matrix: if AAT = In = ATA
18. Idempotent matrix: if A2 = A
19. Involuntary matrix: if A2 = I or A-1 = A
20. Nilpotent matrix: A square matrix A is nilpotent; if Ap = 0, p is an integer.
Trace of Matrix
The trace of a square matrix is the sum of the elements on the main diagonal.
(i) tr(λA_ = λ tr(A)
(ii) tr(A + B) = tr(A) + tr(B)
(iii) tr(AB) = tr(BA)
Properties of Matrix Multiplication
(i) AB ≠ BA
(ii) (AB)C = A(BC)
(iii) A.(B + C) = A.B + A.C
Adjoint of a Matrix:
Inverse of a Matrix :
Matrix Transpose :



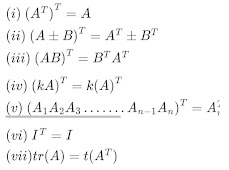

Comments