PERMUTATION AND COMBINATION

The theory of permutaions and combinations is central in problems of counting a large number of objects that are impossible to count manuallly. The theory of permutation  and combinations enables us to count objects without listing or enumerating them .

Permutation :
   Permutation refer to the number of different arrangements of given objects, when the order is important . i.e. A permutaion is an arrangement , in a definite order , of a number of objects , taken some or all at a time.

Formula:

    The formula for permutation of n objects for r selection of objects is given by: P(n,r) = n!/(n-r)!

For example,  the number of ways 3rd and 4th position can be awarded to 10 members is given by:   P(10, 2) = 10!/(10-2)! = 10!/8! = (10.9.8!)/8! = 10 x 9 = 90              

Linear Permutation :

1.  The number of permutation od n different objects taken r at a time when repetition of r objects in the permutation is not allowed is given by 
            

2. The number of permutation of n different objects , taken r objects at a time , when repetition of r objects in the permutation is allowed , is given by n × n × n × ……(r times) = nr

   This is the permutation formula to compute the number of permutations feasible for the choice of “r” items from the “n” objects when repetition is allowed.

3.  The number of permutation of n objects , when p objects are of one kind , q objects are of second kind , r objects are are of third kind and the rest , (if any) ,are of different kind is

Circular Permutation :

The arrangement in a circle are called circular permutation .

1.  The number of circular permutation of n differnt objects = (n - 1)！

2.  The number of ways in which n things of which p are alike , can be arranged in a circular order is 

Combination :

     A combination is a selection. Total number of slection of 'n' deffernt objects, taken 'r' at a time is denoted by  ncr  or nCr or C(n, r) and is given by 
    

Fundamental Counting Principle :

         According to this principle, "If one operation can be performed in ‘m’ ways and there are n ways of performing a second operation, then the number of ways of performing the two operations together is m x n ". This principle can be extended to the case in which the different operation be performed in m, n, p, . . . . . . ways.

In this case the number of ways of performing all the operations one after the other is m ☓n ☓p ☓. . . . . . . . and so on

   
Factorial Notation :

    For a natural number n, the factorial of n, written as n！and read as "n factorial" is the product of n natural numbers from 1 to n.
That is , n！is expressed as 1☓2☓3☓...☓(n -2)☓(n - 1)☓n.

Note :  The factorial notation can also be defined as the product of the natural numbers from n to 1.
That is , n！=  1☓2☓3☓...☓(n -2)☓(n - 1)☓n.
for example.,  6 ！= 1☓2☓3☓4☓5☓6 = 240.

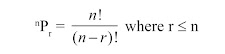
Comments

Post a Comment

Popular posts from this blog

GEOMETRY

     Geometry is one of the oldest branche of mathematics. It is concerned with properties of spaces such as the distance, shapes, size and relative position of figure. A mathematician who works in the field of geometry is called a geometer.      The most common type of geometry are plane geometry (  dealing with objects like the point,line, circle, triangle,and polygon  ) , solid geometry ( dealing with objects like the line, sphere and polyhedron ) , spherical geometry (  dealing with objects like spherical triangl and spherical polygon  ) .      Geometry is used in various daily life application such as art, architecture, engineering, robotics, astronomy, sculptures, space, nature, sports, machines, cars and much more. Geometry is the fourth math course in high school and will guide you through other things like points, planes, angles, parallel lines, triangles, similarity, trigonometry, quadrilaterals, circle, area a...
Read more

LIMITS

Image
 The concept of limit of a function is a fundamental concept in calculus .  Lmit of a Function :          Suppose x is a variable and 'a' is a constant . If x takes value closer and closer to 'a' but not equal to 'a' , then we say that x tends to 'a' . Symbolically it is denoted by x⟶ a .                                we can observ that the value of x are very closed to a but not equal to a .When x > a and x takes values near a , foe example , x = a + 1/8 , x = a +1/4 ... etc, we say that x⟶a +   (x tends to a from larger value ). When x < a and x takes value near a , for example , x = a - 1/2 , a = a - 1/4 , x = a - 1/8 ..etc., then we sat that x⟶ a -  ( x tends to a from smaller value ). Definition of Limits :            Let f(x) is very near to l . This is expressed by |  f(x) - l | <  ε  for any ...
Read more