SETS AND INTERVAL

We know the sets and their types and also know the their operations , let's know the intervals.

Intervals :

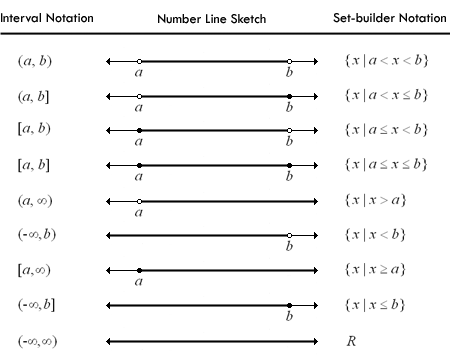
1.    Open Interval :

             Let a ,b ∈ R  and a < b then the set  { x/x ∈ R , a < x < b} is called open  interval and is denoted by        (a ,b)  .All the number between a and b are belongg to this open interval (a ,b) but the number a, b are dose't belong in this interval . 
                      eg ., (3, 8) = {x | 3 < x < 8 }

                

2.   Closed Interval :

              Let a ,b ∈ R  and a < b then the set { x/x ∈ R , a ≤ x ≤ b} is called closed interval  and is denoted by [a, b]. All the number between a and b are belong in this interval [a, b] and also a and b itself are belong in this interval.
     eg.,   [1, 11] = {x | 1 ≤ x ≤ 11 }
 

3.  Semi - Closed Interval :

          Let a ,b ∈ R  and  the set { x/x ∈ R , a ≤ x < b} is called semi - closed interval  and is denoted by [a, b). All the number between a and b are belong in this interval but b dose not belong in th interval
 [a, b) i.e.  a ∈ [a, b)  but b ∉ [a, b) .



4.   Semi - Open Interval:

           Let a ,b ∈ R  and the set { x/x ∈ R , a < x ≤ b} is called semi-open interval and is denoted by       (a, b]. All the number between a and b are belong in this interval but a dose't belong inthis interval .  i.e        b ∈ (a, b]  but a ∉ (a, b] .


5.   i)  The set of all real numbers greater than a i.e. (a, (-∞ , b) = { x/x ∈ R , x < b}) = { x/x ∈ R , x > a}

  
ii) The set of allreal numbers greater then or equal to a  i.e  [a, ∞) = { x/x ∈ R , x ≥ a}     


6.  i) The set all real numbers less then b i.e. (-∞ , b) = { x/x ∈ R , x < b}


 ii) The set of alll real number less then or equal to b i.e (-∞ , b] = { x/x ∈ R , x ≤ b}    



7.     The set of all real numbers R is (-∞ , ∞) = {x /x ∈ R , -∞ < x < ∞}
        

Infinite intervals :  are those that do not have an endpoint in either the positive or negative direction, or both. The interval extends forever in that direction. Infinite intervals are summarized in the table below.


Comments

Post a Comment

Popular posts from this blog

Mathematics

INTRODUCTION                      Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes.                  The basis of the earliest contribution, the father of  mathematics is Pythagoras. Because Pythagoras is described as the first pure mathematician .  He is an extremely important figure in the development of mathematics.         And also Aryabhatta is the father of Indian Mathematics. He's major work's in  spherical trigonometry, plane trigonometry and determined the value of π correct to four decimal places. Aryabhatta also found the zero (0).      BASIC RULE OF MATHEMATICS    BODMAS is the basic rule of mathematics     According to BODMAS rule, the bracket have to be solv...
Read more

PERMUTATION AND COMBINATION

Image
The theory of permutaions and combinations is central in problems of counting a large number of objects that are impossible to count manuallly. The theory of permutation  and combinations enables us to count objects without listing or enumerating them . Permutation :    Permutation refer to the number of different arrangements of given objects, when the order is important . i.e. A permutaion is an arrangement , in a definite order , of a number of objects , taken some or all at a time. Formula:      The formula for permutation of n objects for r selection of objects is given by:   P(n,r) = n!/(n-r)! For example,   the number of ways 3rd and 4th position can be awarded to 10 members is given by:    P(10, 2) = 10!/(10-2)! = 10!/8! = (10.9.8!)/8! = 10 x 9 = 90               Linear Permutation : 1.  The number of permutation od n different objects taken r at a time when repetition of r object...
Read more

Circle

Image
Definition :         A circle is a set of all points in a plane which are equidistant a fixed point in the plane . A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “centre”. Every line that passes through the circle forms the line of reflection symmetry. Also, it has rotational symmetry around the centre for every angle. The circle formula in the plane is given as: (x-h) 2  + (y-k) 2  = r 2 where (x,y) are the coordinate points (h,k) is the coordinate of the centre of a circle and r is the radius of a circle. Circle Shaped Objects There are many objects we have seen in the real world that are circular in shape. Some of the examples are: Ring CD/Disc Bangles Coins Wheels Button Dartboard Hula hoop Parts of Circle Annulus - The region bounded by two concentric circles. It is basically a ring-shaped object. See the figure below. Arc –  It is basically the connected cu...
Read more